|
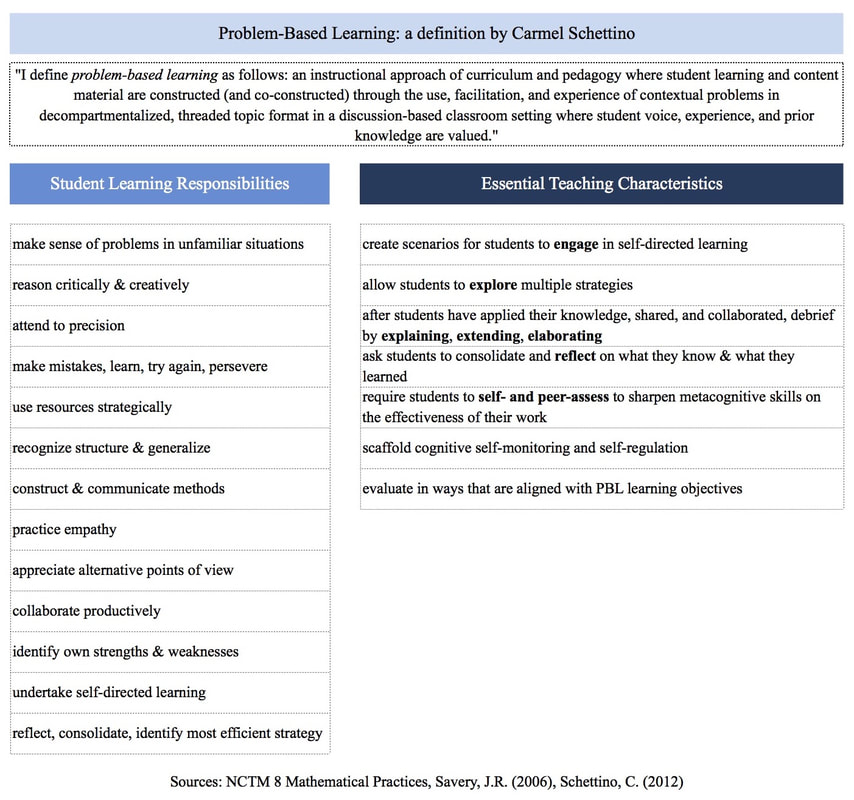
by Taylor Wyatt After reading several articles this week, I wanted to summarize and share the chart I made to remind me of the essentials for teaching and learning in a PBL classroom. I like the idea of sharing it with my students to "pull the curtain back" and clarify our roles. Reactions? Ideas? Improvements? If you want to read into these characteristics, I recommend the following: Engaging in the 8 NCTM Mathematical Practices Teaching Geometry through Problem Based Learning by Carmel Schettino Overview of Problem-based Learning: Definitions and Distinctions by John R. Savery
0 Comments
by Rachel Van Wickle What is it that creates a classroom environment where students feel supported and believed in, and safe enough to take risks without fear of failure? In past years, it has felt like some of my classes have had this “magic” while others have not. How can I break the magic down into tangible and repeatable steps? I’m thinking that constructing classroom values is one step in the right direction. In my Integrated Problem Solving II course this year, I experimented with the first three days to try to create a sense of safety and belonging. I did so by first presenting my values as teacher, then asking students to journal about their individual values, and finishing with a discussion of values for our class as a whole. Later in the term, we revisited our class values and reflected on what might be added or adjusted. Here is what it looked like: Day 1 – Teacher Values On the first day of class, I presented my students with the following: We discussed why these values are important to me as a math teacher, and I explained how my grading and assessment policies align. To drive the message home, I asked the students to take about five minutes to journal a response to the prompt, “Why are mistakes important?” This idea came from Jo Boaler’s course, “How to Learn Math For Teachers.” Here are the main themes that I took from discussing mistakes with my students:
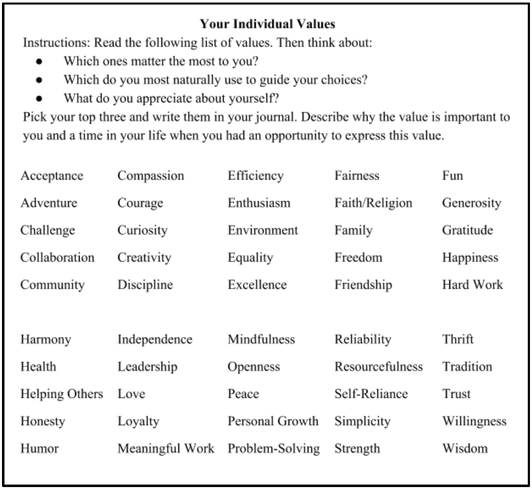
Day 2 – Individual Values On the second day of class, I asked students to journal about their own values. This prompt came from math department member, Taylor Donovan Wyatt, and allowed students an opportunity to be specific about how they view themselves as a member of the class. Here is the exercise, followed by three student examples: A question I have after conducting this activity is whether or not to ask students to share these with each other. Do they gain the feeling of safety and belonging from this activity merely by me reading and responding to their journal entry? Would it be asking them to be too vulnerable to share out as a class? Or, would sharing them with each other create an even better sense of community? Below are three student examples that show the variety and scope of the exercise.  Day 3 – Class Values On the third day of school, I asked students to partner up and discuss what values we should set in place for our class so that our discussions for the rest of the year would be as successful as possible. After sharing out, we compiled the list shown at the right. I then posted this list on the main page of our LMS so that we could refer back to it as the year progressed. Because the students all agreed to this list on day 3, I was able to hold each student accountable so that everyone in the class would feel supported and encouraged.  Day 40 – Revisiting Values On the first day of the second term, I brought out the list of class values that we created on day 3. I asked students to reflect on which of these values was a strength for our class in the first trimester and which, if any, we could work on more. Students also used this exercise as an opportunity to add and revise our list since so much time had gone by since it was first created. I find it interesting that the student in the example below uses the word “we” to discuss the growth of our class as a whole. Then, she finished writing by detailing how the class dynamic affected her own individual experience. Here is what she wrote: All in all, I am excited to use this sequence at the beginning of next year, but I am definitely interested in adjusting it to better serve my students. Is this too touchy feely to start math class with? How do I encourage students to be authentic right at the start of the year? What else should be done as the year progresses to revisit the values and continue cultivating the sense of safety and belonging???
By Annalee Salcedo
I had the pleasure of formally observing two PBL classes recently. As a window into what our Integrated Problem Solving courses look like, I share here excerpts of my observation write-ups of these two classes. IPS 2: C Block, Teacher: Taylor W. This class, as expected had a high ratio of student to teacher voice. Students were constantly talking to each other about math. Sitting in a circle, students were leaning over to neighbors, and talking across the circle to discuss with their peers the tests that they had just gotten back. Taylor seemed just another member of the circle, talking about math with a neighbor. Her input was not solicited any more than any other active student, and her neighbors easily turned the other way to talk to a peer when they were done talking with Taylor. What the students were saying as they reviewed their work and their mistakes on the test was also a model for what I'd hope students in all our classes are saying: "I struggled through it then I got it." "It made me so happy." "That was hard!" "That makes sense" "Wait, I need to think." "I enjoyed this problem." When discussing homework problems, and recognizing the opportunity to apply various methods they've seen before, I heard students say: "I like the Shion method." or "I like the Yuki method." The students themselves are clearly sources of knowledge and techniques for each other, rather than the teacher or the textbook. The students associate problem solving strategies that they can use with the work that other students have shown them. Taylor spoke more during the discussion of the HW problems. But her comments were about bringing attention to key points: emphasizing the introduction of notation, asking students to generalize an outcome of a problem. After the Midline Theorem problem, for example, no fewer than five students chimed in to try to articulate what the problem showed them. They built on each other's comments and finally arrived at a clear theorem they could put in their "What we know about Geometry" document. A 6th student noted that the theorem was "pretty rad." IPS 2: A Block; Teacher - Rachel VW. Rachel sets a clear expectation that math can be / is enjoyable. Her opening questions about the homework were "Did we have any favorites?" and "What are we most looking forward to?" After those opening questions, most of the comments/discussion featured student voices. Students are clearly used to the culture of responding to each other's work, raising questions, showing different ways of approaching the problem, and even thanking each other for pointing out mistakes! One student who presented knew to check for understanding from his peers, stopping at a point in his presentation to say, "Sound good?" or “Do we all agree?” Another student started her presentation by listing what she noticed about the problem. A different student took the results of one problem and asked the group if they thought it generalized to all right triangles. Another student noted that it generalized to all triangles, not just right triangles. On a different problem, one student was able to identify an assumption he made that led him astray. A different student recognized he was about to make the same mistake as a classmate did, and noted that he remembered discussing her mistake and that helped him avoid it. There's clearly a culture of learning from mistakes and seeing them as valuable, and probably in part a result of Rachel’s explicit valuing of mistakes: "I saw some great mistakes." Overall, two great classes to observe because the students were so active and vocal. It wasn't so much teaching I got to see, but the process by which students were learning themselves. But of course, the environment is set by the teacher, and I appreciate the thoughtfulness, purpose, skill behind Taylor’s and Rachel’s moves that make such a learning environment possible for their students. This fall our students began working through Exeter's Math 2 PBL curriculum, all but one of them trying this style of learning for the first time. I asked my class to reflect on their experience as the term ended. They describe their ups and downs as both challenging and exciting, offer a little advice, and generally show off for me (I'm waaay lucky to work with these thoughtful, honest, and purposeful students). I like how they emphasize the difficulty of genuine learning, while at the same time owning the valuable results. by Annalee Salcedo Here’s a note my student, Hunter, wrote to me on the bottom of his quiz yesterday, in response to my question: “How can I make math class so it’s more like ceramics class?” Back story:
A few weeks ago, our ceramics teacher, John, announced he’d be offering an adult ceramics course on Saturday mornings to any interested faculty members. I signed up and so did several others, filling the class almost immediately. In our first class, John showed us around the ceramics studio, where to get the clay, how to wedge it, where various hand tools are and how they’re used. He demonstrated how to center, throw, pull and trim a bowl. Then he set us loose on the clay and told us to give it a try. I returned to the ceramics studio later that afternoon, and again the next day and the next day and the next day, every day trying to center, throw and pull a piece of clay into something, anything. When I messed up, I could throw the clay into the slip bucket, clean off my bat, and start over with another piece of clay. There were literally no stakes to making mistakes and this motivated me to just keep trying. A few days into my new obsession, I decided it would be interesting to observe my learning process. Here’s what I noticed about how I was learning:
Often, when I’m in the ceramics studio, there are students in there, too. They come not only when their ceramics class is scheduled, but also before sports, after dinner, when they’re done with homework for other classes, on Sunday afternoons. Today there was a student there who’s not actually in ceramics, but she was curious and interested and thought she’d give it a try. Other students who are in the ceramics course were coaching her. I’m finding that students are always eager to share their tips for centering, pulling, or trimming when I ask for their advice, and in the very beginning, some even offered unsolicited help because clearly I needed it. I shared these observations about my learning and about the culture of the ceramics studio with John and asked him the same question I had asked Hunter. How do I set up math class so it’s more like his truly student-driven ceramics class? John admitted that he didn’t have an answer, but acknowledged that teaching ceramics is way easier than teaching history, which he used to do. I see Hunter in the studio often, and he had asked about the adult class - when it happens, who’s in it, and he commented that he thought it was pretty cool to see teachers in the studio trying hard. So when he arrived to honors pre-calculus early today with clay smears on his pants and shirt, I asked him how I could set up math class so that it was more like ceramics. This started a flurry of ideas among the other students who had also arrived early. “You could just give us projects and let us figure stuff out”, said one student. “But how would we know if we were right?” asked another. “How do you know if what you made in ceramics was ‘right’?” I asked. “Well, there is no right or wrong in ceramics, just what you like,” someone else replied. “But in math, we have stuff we need to know,” said the student who needed to know if she was right. “Does ceramics have content standards?” I asked. “No.” “Actually, yes,” said Hunter. “Our bowls have to meet certain criteria. The shape inside should the same as the shape outside. The foot is one third the diameter.” As the bell rang to begin math class, I wondered if Hunter could state the criteria for success in our unit on trig as readily and clearly as he could for the unit on bowls in ceramics…Likely not, but more because of how I’ve set the unit up, and not because Hunter’s not paying attention. In fact, Hunter is actually quite a metacognitive thinker, as evidenced by his note that inspired this blog post in the first place. I collected the quizzes and it wasn't until I was on dorm duty tonight grading them that I saw that Hunter took some time after he'd finished and while others were still working to respond in writing to my question. It tells me he finds it as compelling a question as I do. What Hunter wrote resonates with me and I’m going to keep thinking about it: Start with “desired skill” then “youtube, practice, mistakes, epiphany [sic], mistakes, repeat.” This is exactly how I would describe my process as a learner in ceramics, and it has been an incredibly enriching experience so far. What can I do to set this process into motion for my students as they learn math? (Please comment if you have ideas!) by Annalee Salcedo They say that if you come back from a professional development conference and don’t use what you learned in your class within two weeks, you’re likely not to use it at all. So on the plane ride from Phoenix, where I just spent two and a half days at Solution Tree’s Annual Conference on Grading and Assessment, I planned how to incorporate at least a little of what I had learned into my classes. I have been dappling with standard based grading for the last few years, but the Conference gave me language (and confidence) that I was able to use immediately in my parent-teacher conferences, which started less than three hours after I landed in Santa Barbara and returned to Cate. During our conferences, I showed parents their child’s row in my gradebook (excerpted below), which tracked each student’s progress on the learning objectives for the term, listed across the top. I explained how their child’s grade reflects their level of proficiency (on a 1-4 scale) with these objectives at this time. I showed them how most of these skills have already been assessed at least two or three times, and how their score for each skill (in white columns) more heavily reflects their most recent performance rather than scores from when the skills were just introduced. “That makes total sense,” parents said all night. In most of my conferences, I was able to point out to the parents that their child improved on several skills (for example, Student 1’s improving ability to interpret rate functions), and I could see the pride and approval in the parents’ faces. In a few cases, the parents noticed before I could point it out that their child got several “2”s in a row and they said, “hmm, my child isn’t learning from his mistakes.” In most of these conferences, we didn’t talk about grades - we got to talk about how well our students are learning.
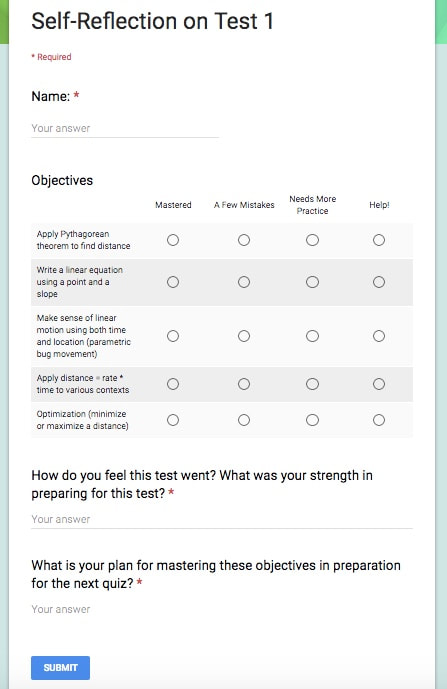
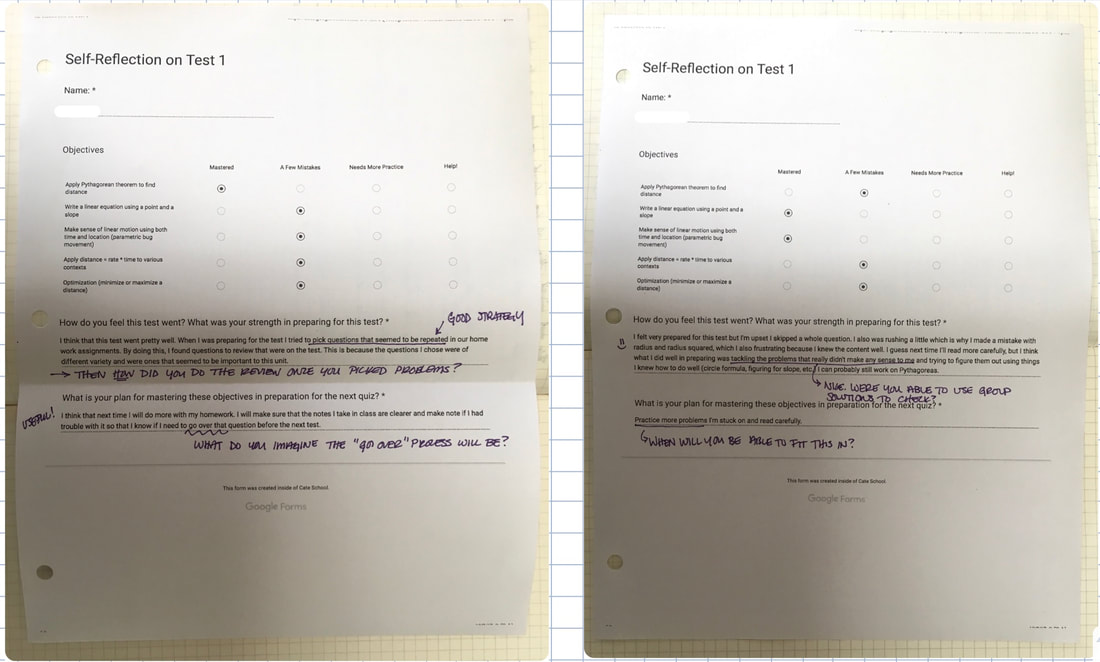
Bill Ferriter was a one of the speakers at the Annual Conference on Assessment and Grading and in his book, “Creating a Culture of Feedback” he quotes Seymour Papert who wrote, “The skills that you can learn when you’re at school will not be applicable. They will be obsolete by the time you get into the workplace and need them, except for one skill. The one really competitive skill is the skill of being able to learn.” My conferences last night were all about how well students were learning. Parents were asking, “Does my child know what the learning goals are?” “Does my child know where she is on that skill?” “Is he using your feedback?” “Is she checking in with you to make sure she knows what she needs to do to improve?” I did have one parent persist in a line of questioning specifically about what in terms of content his child needed to do better in order to be more successful in this class. The student had gotten a string of 3s and 4s on the most recent assessment of our target skills to date, and so I said that in fact, mathematically he’s shown solid levels of proficiency. But we noticed that all previous assessments were riddled with repeated 1s and 2s, so clearly this student prepared really well for the unit test, but wasn’t addressing the mistakes during the unit. I was able to explain to the parent that in terms of product, his son was able to deliver, but his process clearly needed improvement. The parent said, “Oh, so it’s not just math you’re trying to teach him. OK, I’ll talk to him about that.” So will I, I promised. Part of why I felt ready to jump into these conversations with parents just hours after the end of the Assessment and Grading Conference is because I realized that though I’m not using a full fledged standard based grading system, I have fully adopted the Standards Based Mindset, which Tom Schimmer spoke about at the Conference. It was super exciting to share this mindset and evidence of their student’s learning habits with parents during our conferences. I did have one student attend his meeting with his parents (and I love it when they do that!). But it revealed to me some of the work I have yet to do. For example, my student wasn’t able to describe this system of assessment and grading, even though I had explained it in class and had them read about it on our class website. (Classic: if they didn’t learn it, did I really teach it?). He didn’t know how my google sheet worked, what the 1-4 scale meant, or how this all mapped to a letter grade in the end. This tells me I need to get my students more actively involved our system of assessment. As Ferriter puts it, I need to teach my students how to gather feedback rather than wait for it from me, as if I were the expert on their learning. I need to figure out ways to get my students actively judging their own levels of proficiency, tracking their own progress, and identifying next steps for themselves. Luckily, Ferriter’s book has lots of great practical tips for how to teach students to become experts in their own learning. Those are the tips I was taking notes on during my plane ride from Phoenix, and I can’t wait to start using them! by Taylor Donovan Wyatt Last week my students went through the testing process for the first time. Because our curriculum is written so that topics are interwoven and spiral in difficulty, preparing students for a test is something of a decoding process. The various “threads” are usually obvious to the teacher, but for students, the unraveling of topics can be like "the big reveal" in a renovation show. In my class last week, each student took responsibility for five problems, listing topics covered and writing up “solution guides” to share with their classmates. In this particular problem set, one student listed topics including “Pythagorean Theorem,” “Circle Formula,” and “Find Distance Between Two Points.” Another student reacted, saying, “Hey, can we just call that category ‘Pythag?’” Some classmates were all in favor, others resistant, but the discussion that followed about why -- or why not -- these problems could be grouped was really encouraging. Other topic connections were explored as well, like the relationship between problems involving linear graphs, equations, and tables. Students also listed problem-solving strategies and attached them to problems: “Use two different methods to check this problem - algebra and graphing,” or “make a chart to show patterns.” Though I prompted students throughout discussion, my role was primarily as note-taker as the class took ownership for what would be on the test. After the test, a six problem affair that closely resembled the questions they’ve been working on in class or at home, students were asked to do an objectives-based reflection. Rachel came up with this idea a few years ago and it is so useful. She created a google form listing the objectives tested (unconnected to problem numbers). Students must match their performance on certain problems with the objective and rank themselves on a scale from “mastery” to “I need help.” Then, they answer two short questions on their test experience and how they plan to prepare for the next assessment. Because our students are younger, many of them wrote earnest, but vague responses in their reflections. So we printed out their individual responses, taped it into their journal, and asked questions like “What do you mean when you say, ‘go over problem 2 again’? Would you like to meet for 10 minutes? When? How will you practice unit conversions?” Students then had an opportunity to get more specific. We teachers also learned a lot about what students find challenging in terms of our course objectives, how students actually prepared for the test, and how they plan to improve or continue their preparation process. Two examples are below. What are the strengths of your PBL testing process? What could we do differently or better? Thank you for reading, Taylor.
|
Authors
Taylor Wyatt Archives
May 2018
Categories |








 RSS Feed
RSS Feed
